Matematik åk 7 kap 3

Vinklar
omkrets
skala

Matteord:

vinkelben                                         parallellogram

vinkelsumma                                   romb

rät vinkel                                          diagonal

spetsig vinkel                                  omkrets

trubbig vinkel                                  cirkel

rak vinkel                                         medelpunkt

rätvinklig triangel                           radie

likbent triangel                               diameter

liksidig triangel                              skala

kvadrat                                           förminskning

rektangel                                        förstoring

                                                        naturlig storlek

Mål

- uppskatta, mäta och räkna ut vinklar i olika geometriska figurer

- använda gradskiva

- räkna ut vinklar med hjälp av vinkelsumman i en triangel

- beskriva olika slags trianglar och fyrhörningar

- mäta och räkna ut omkretsen olika geometriska figurer

- räkna med skala

 

Tidsplanering:

Vecka       Grön/Röd kurs         Blå kurs           Uppgift     

47             Sid 70-76              Sid 86,87         Trianglar

48               Sid 77-78              Sid 88              Fyrhörningar, omkrets                 

49               Sid 89, 79-80        Sid 80, 89        Cirklar

50              Sid 81-83              Sid 90-91         Skala och diagnos           

51              Förbereda för prov och provvecka

 

Exempeluppgifter E-A:nivå:

Åk 7 exempeluppgifter till PROV 3

 

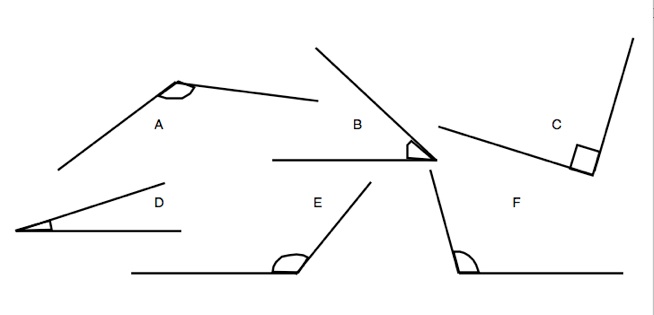
 1. Hur stora är vinklarna, mät med gradskiva. 

 

 

 

 

2.Rita en spetsig vinkel.

3.Hur många grader är en rät vinkel?

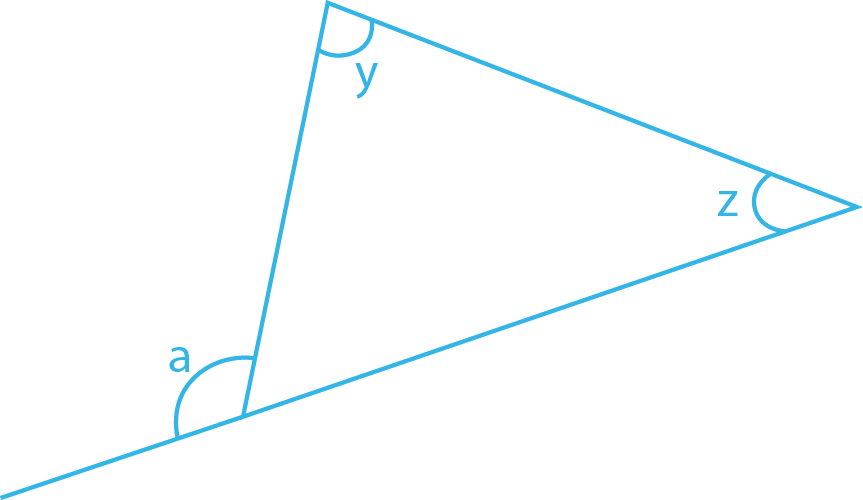
4. räkna ut vinkeln a om z=40 och y=80

                                                                                                                                      

 

5. Vilka av trianglarna är:

a) rätvinkliga

b) likbenta

 

6. vilka av figurerna är

a) parallellogram

b) romb

c) rektangel

7. Vilka påståenden är sanna?

a) I en romb är alla sidor lika långa.

b) I en liksidig triangel är alla vinklar 60

c) I en rätvinklig triangel är två av vinklarna räta.

 

 

 

 

Videolektioner

vinklar:

https://www.youtube.com/watch?v=tP30777con8 

IT-övningar/uppgifter:

ur mattelyftet Modul:GE

https://matematiklyftet.skolverket.se/matematik/content/conn/ContentServer/uuid/dDocName:LI64RH5PRO020442?rendition=web